It has been a while since I posted anything on this blog space. Today, we are going to go over some binary tree traversal types together.
The easiest way we can come out with is by doing recursion. Before we get to the code, let's revisit what preorder, inorder and postorder traversal is.
For preorder traversal, the sequence of node visit is curr - left - right.
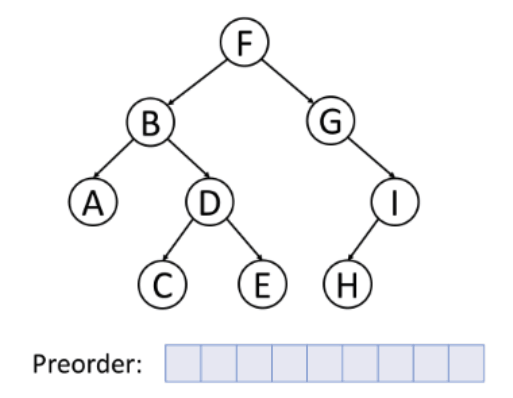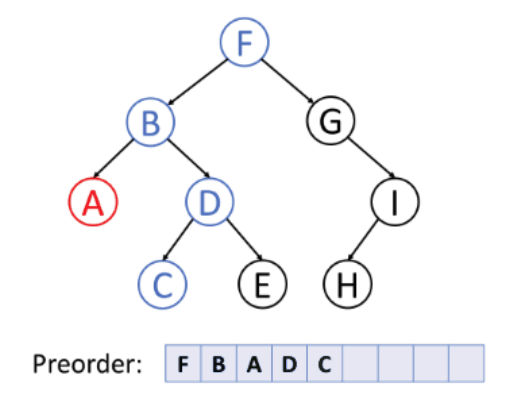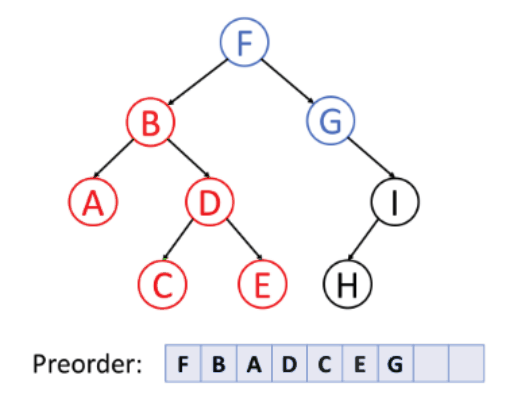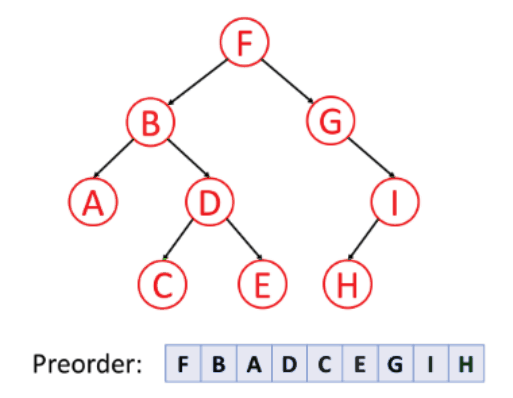
For inorder traversal, it goes from node left - curr - right.
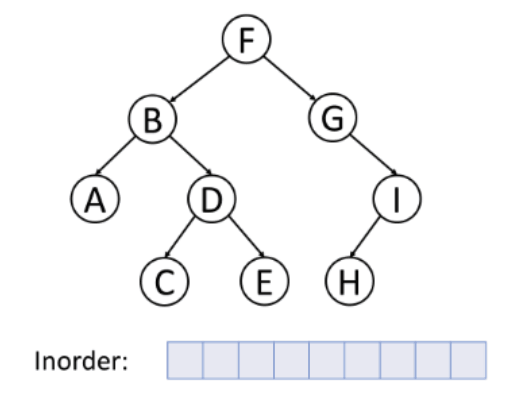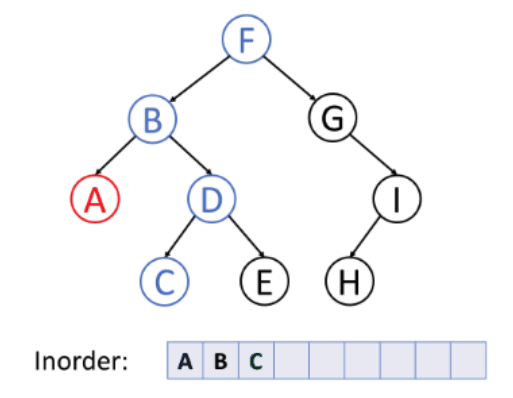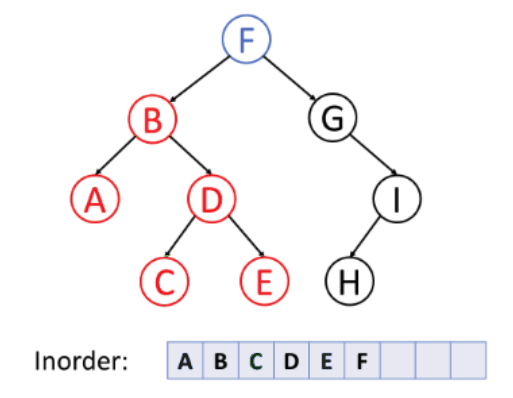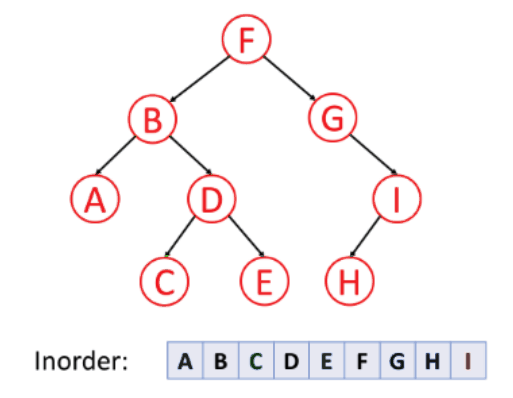
For postorder traversal, it goes from node left - right - curr.
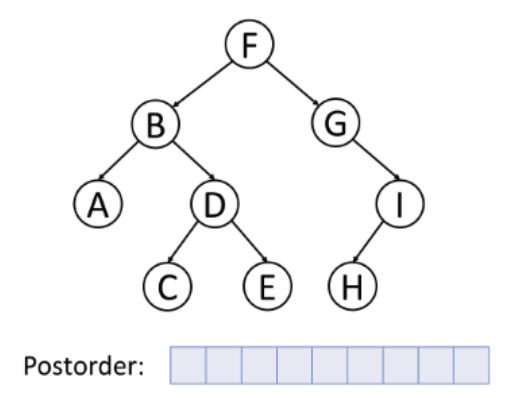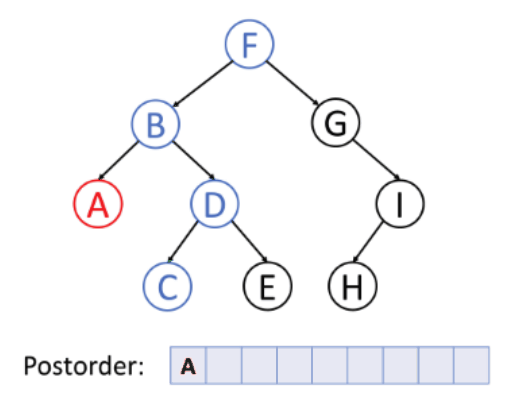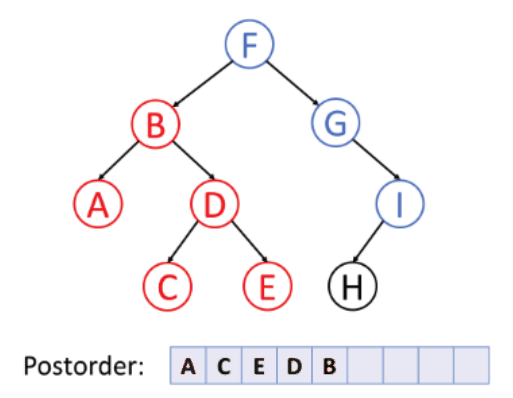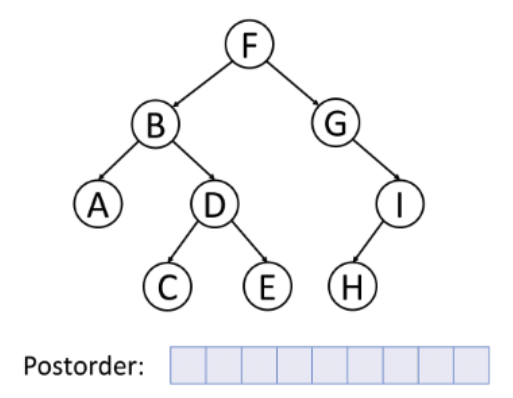
The basic code snippet for preorder traversal is shown as below:
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> list = new ArrayList<>();
helper(root, list);
return list;
}
private void helper(TreeNode root, List<Integer> list){
if(root == null){
return;
}
list.add(root.val);
helper(root.left, list);
helper(root.right, list);
}
For inorder traversal, you just need to swap these two lines:
...
helper(root.left, list):
list.add(root.val);
helper(root.right, list);
...
And for postorder traversal:
...
helper(root.left, list);
helper(root.right, list);
list.add(root.val);
...
The solution provided above is the famous binary tree traversal in recursive way. The essence of this problem is not to solve it recursively but also in iterative manner. For this particular question, we can also solve it by making use of Stack data structure.
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> list = new ArrayList<>();
if(root == null){
return list;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
list.add(node.val);
if(node.right != null){
stack.push(node.right);
}
if(node.left != null){
stack.push(node.left);
}
}
return list;
}
For preorder traversal, first we put in the root node into the stack. Then, we check if the node has left or right nodes, push them into the stack if the node is not null. While the stack is not empty, we continue popping out the last element and pushing in the child nodes. Once the stack is out of element, we can simply return the list.
NOTE: We push in right node first instead of left node because stack is a LIFO data structure that the last entered element gets to pop out first, which in this case is exactly what we want for the left node to pop out first.
As for inorder traversal, the process flow is slightly different than the preorder traversal. First, we need to make sure the node keep traversing to the leftmost node and while traversing to the leftmost node, we push the current node along the way. When there is no more node to visit, we pop out the last entered node and set the current node as the the right child node. The code snippet is shown as below:
public List<Integer> inorderTraversal(TreeNode root){
List<Integer> list = new ArrayList<>();
if(root == null){
return list;
}
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()){
while(root != null){
stack.push(root);
root = root.left;
}
root = stack.pop();
list.add(root.val);
root = root.right;
}
return list;
}
Lastly, the postoder traversal is very similar to preorder traversal. What difference is that the node is added at the beginning of the list instead of the end. Also, the sequence of adding left-right node is left node first then right node later. See the code snippet below:
public List<Integer> postorderTraversal(TreeNode root){
List<Integer> list = new ArrayList<>();
if(root == null){
return list;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
list.add(0, node.val);
if(node.left != null){
stack.push(node.left);
}
if(node.right != null){
stack.push(node.right);
}
}
return list;
}
Lastly, binary tree traversal can be done by divide and conquer method as well. The divide and conquer method for preorder traversal is shown as the following:
public List<Integer> inorderTraversal(TreeNode root){
List<Integer> list = new ArrayList<>();
if(root != null){
list.add(root.val);
list.addAll(inorderTraversal(root.left));
list.addAll(inorderTraversal(root.right));
}
return list;
}
Likewise, the inorder traversal is just swapping these few lines of code:
...
list.addAll(inorderTraversal(root.left));
list.add(root.val);
list.addAll(inorderTraversal(root.right));
...
And the postorder traversal:
...
list.addAll(inorderTraversal(root.left));
list.addAll(inorderTraversal(root.right));
list.add(root.val);
...
Hope this post helps with binary tree traversal. That's it for now, see you all in next post!
Post was published on , last updated on .
Like the content? Support the author by paypal.me!


